Data Science Notes

K-means clustering

Table of contents:

Introduction

K-Means clustering is one of simplest clustering algorithm, so for it is highly recommended to be known for everyone intended to work with Machine Learning.
It was invented by Stuart Lloyd in 1957 (published in 1982) and E. W. Forgy in 1965 independently, therefore the algorithm is very often referred to as the Lloyd-Forgy algorithm.
The aim of the algorithm is to group n objects into k clusters while minimizing the variance within clusters. From the previous follows that K-means is a partitional algorithm (it breaks the dataset up into different groups).

Algorithm

1. Randomly select **k** points as cluster center from the input space
2. Do
	2.1. Assign each datapoint to the closest cluster center
	2.2. Compute new centers based on the given partitions (clusters with datapoints)
3. Until convergence

The algorithm consists two main steps: The assignment step (step 2.1) and the Update step (step 2.2).

  1. Assignment step:
    • Distance function is used to decide which center is closest to a given datapoint. One feasible choice for the distance function is the Euclidean distance (other reasonable distance function are fine as well such as Manhattan distance, Sum of Squares, etc.).
  2. Update step:
    • The new cluster center is the centroid of the datapoints in the given cluster.

The algorithm is visually represented below:

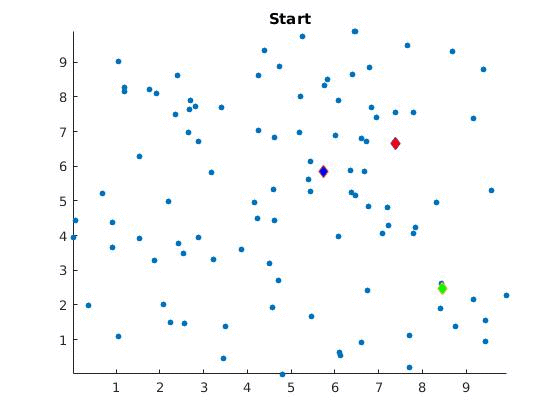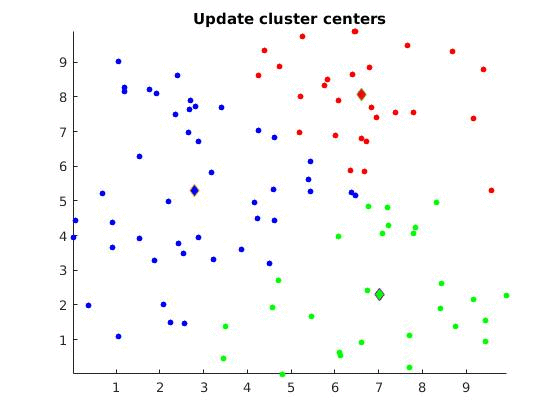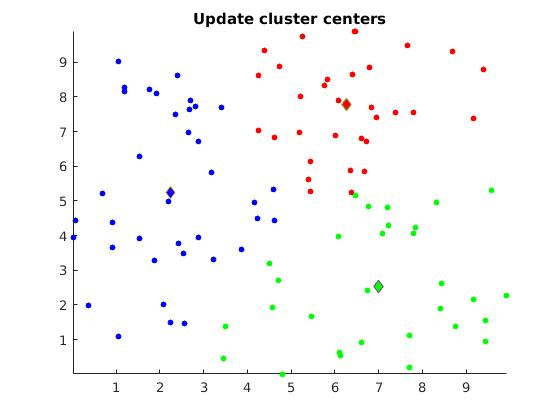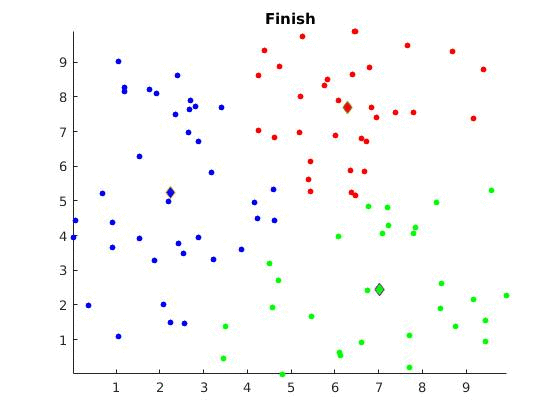
kmeans algorithm

Discussion

Advantages

  • Efficient: \( \mathcal{O}(k \cdot n) \) per iteration
  • Easy to implement, and so is very popular

Disadvantages

  • Converges towards a local minimum
  • Sensitive to outliers and noise
  • Hard to determine number of k clusters
  • Strongly dependent on the initial random cluster center selection (both in result quality and runtime)
  • Relies on the assumption that clusters are convex

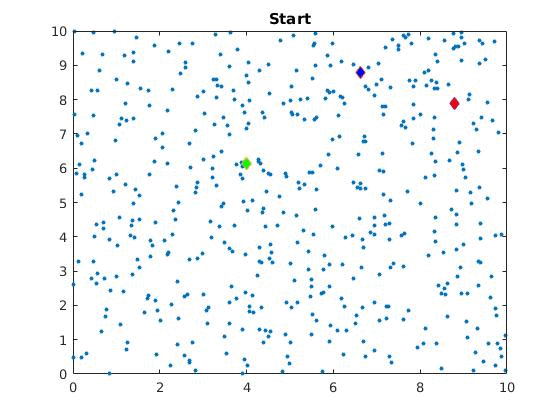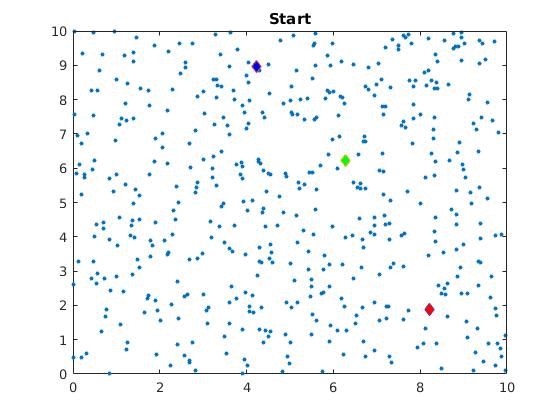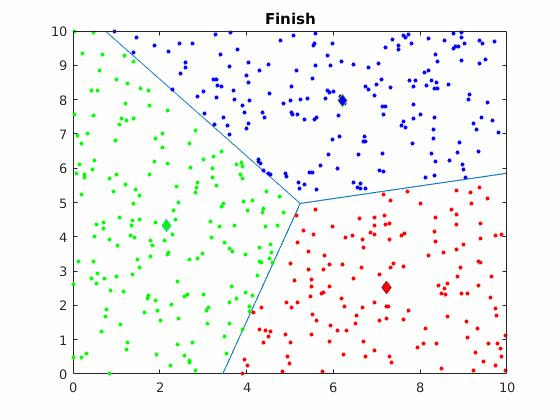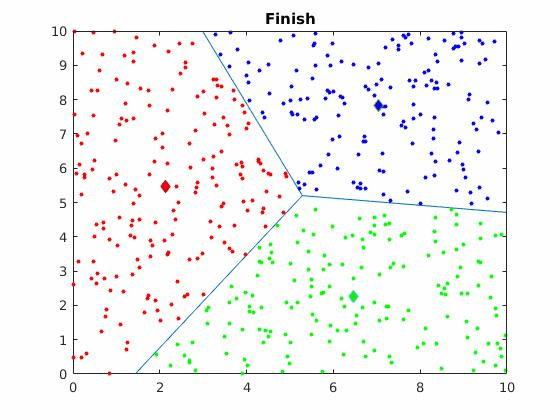
Below you can see how the clustering changes for different initial cluster centers on the same dataset. kmeans different convergence

The K-means algorithm has inspired many researchers and practitioners, so there exist several variations and other algorithms, which are based on the idea of the K-means algorithm.
For example the K-medians and K-medoids algorithm, which differs from K-means only in step 2.2 (how the new cluster center is calculated) and step 1 (the initialization of the cluster representatives) from the previously presented idea.

In K-medoids, we randomly select k initial cluster representatives (medoids) from the dataset. Then, assign each point to the closest medoid and calculate the total cost of the configuration. Thereafter, we check for each medoids variation the total cost of the given configuration and choose the one with the lowest score.
Note that a medoid must be a member of the dataset

You can find appendices for this algorithm here:

Examples

You can find the corresponding scripts (if applicable), here:

comments powered by Disqus